Normale standaardverdeling

Schietschijf

Er worden heel veel schoten afgevuurd op een hele grote schietschijf, die uit allemaal ringen bestaat. 

Er is ook een assenstelsel getekend op de schietschijf met de oorsprong in het middelpunt.

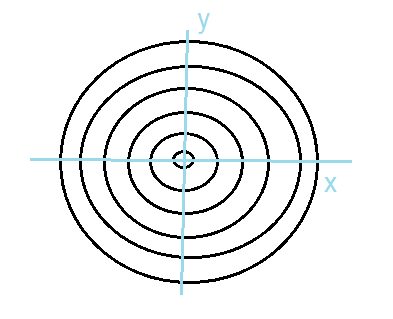
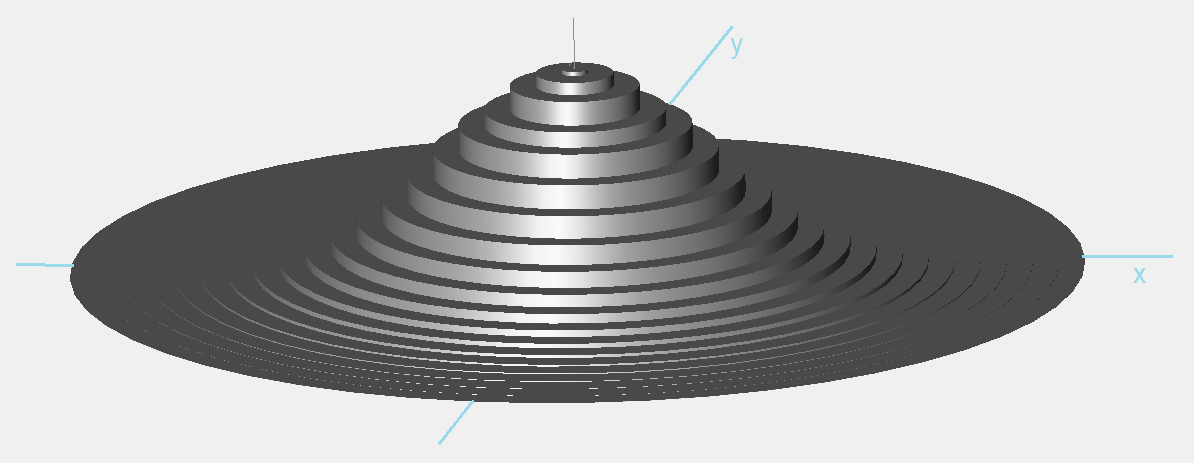
Als we bijhouden hoeveel treffers er op een bepaalde positie (x,y) terechtkomen, dan kunnen we het aantal treffers uitzetten tegen de x- en de y-waarden van elke positie.

We verkrijgen op deze manier een 2-dimensionale verdeling, die een klokvorm heeft.

 

 

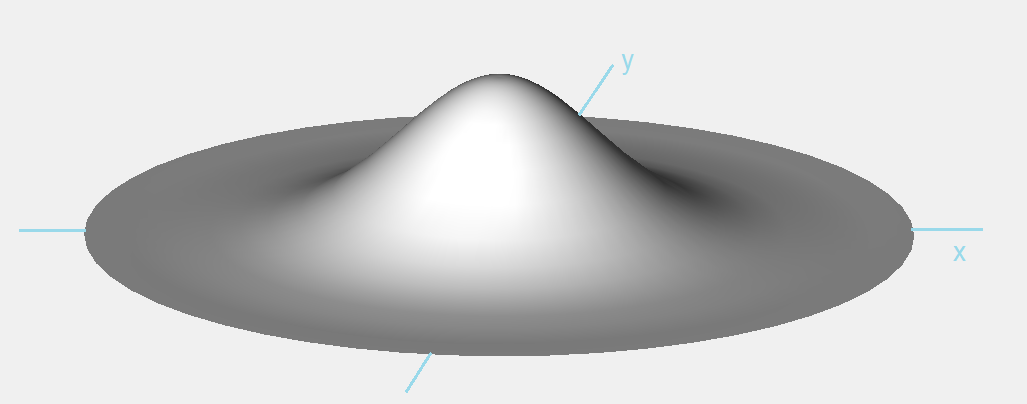
1-dimensionale verdeling

Bekijken we de verdeling die zich boven de x-as bevindt, dan zien we hier een 1-dimensionale verdeling voor het aantal treffers met een bepaalde x-waarde. (de y-waarden doen er even niet toe)

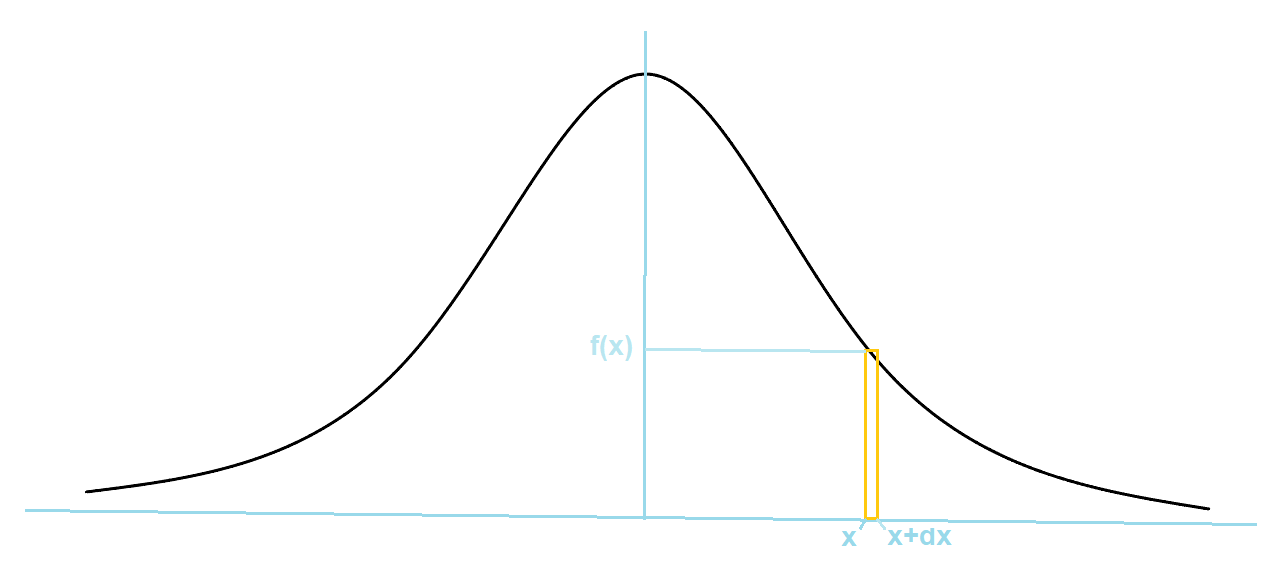
De oppervlak van de curve is het totaal aantal treffers n_tot op de schietschijf.

n(x) = het aantal deeltjes dat tussen de waarde x en x+dx ligt.

De kans P dat er treffers zijn tussen x en x+dx is:

Normalisatie

De normale standaardverdeling is genormaliseerd, d.w.z. dat het oppervlakte van de curve precies 1 is.

Hiervoor moeten we de verdeling voor het aantal treffers door n_tot delen.

f(x) = de functie van de genormaliseerde standaardverdeling, oftewel de normale standaardverdeling.

De kans P dat er treffers zijn tussen x en x+dx is:

f(x) is dus eigenlijk de kansdichtheid.

Er geldt ook:

2-dimensionale verdeling

Hoe groot is de kans dat er treffers zijn tussen x en x+dx, maar ook tussen y en y+dy ?

De verdeling voor de y-waarden is hetzelfde als voor de x-waarden, en heeft ook dezelfde functie f.

De kans is niet meer een oppervlakte van een strookje, maar een volume van een staafje.

Het staafje heeft als grondoppervlakte dx*dy en hoogte f(x)f(y)

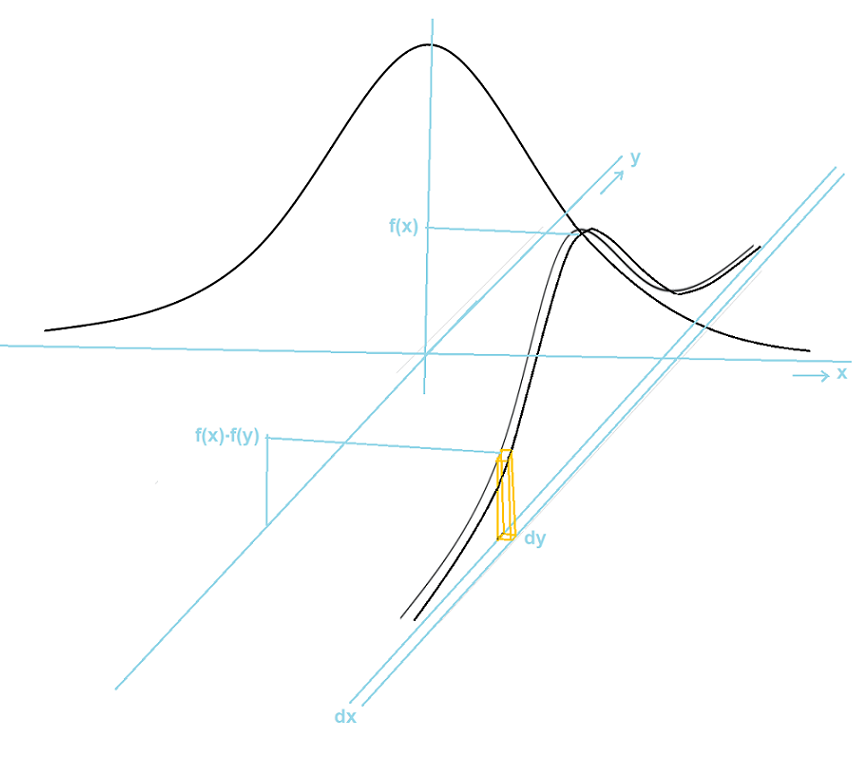
De afstand van het middelpunt (oorsprong) tot aan het punt (x,y) is straal r.

Maar er zijn nog meer punten (x,y) die allemaal dezelfde straal r hebben en dezelfde kansdichtheid f(r).

Al deze punten bevinden zich op een ring.

 

 

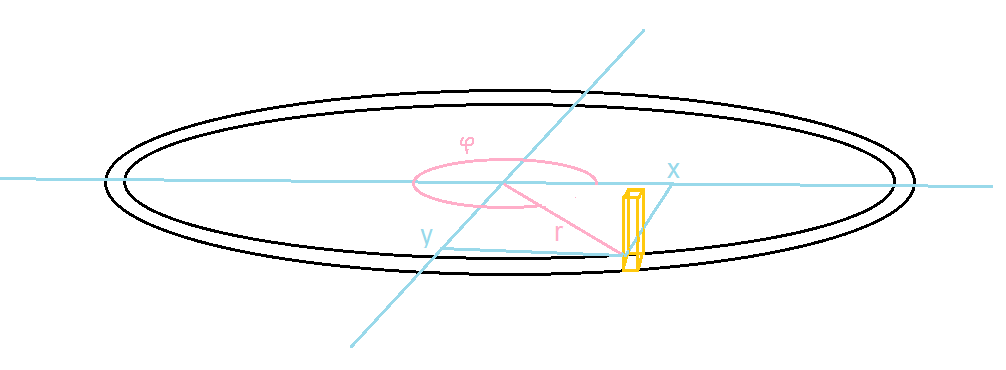
Hoekonafhankelijk

De functie f(r ) is voor elk hoek ϕ gelijk.

Bij differentiatie over de hoek ϕ geldt:

 

Productregel toepassen:

Uitgaande van:

dan geldt voor de afgeleiden:

Nu kan geschreven worden:

Er wordt nu gedeeld worden door xyf(x)f(y)

Scheiding der variabelen:

Aan elke kant hebben we een differentiaalvergelijking die als een constante k beschouwd kan worden.

Wederom 1-dimensionale verdeling

Kijken we alleen naar de x-waarden, dan krijgen we:

Om dit op te lossen moeten we integreren:

De oplossing is:

Hieruit volgt:

Deze functie f(x)=0 bij x=-∞ en bij x=∞, en daarbij moet constante k negatief zijn.